Die Inferenzstatistik ist ein Zweig der Statistik, der sich mit dem Ziehen von Schlussfolgerungen über eine Population aus einer Stichprobe befasst. Im Gegensatz zur deskriptiven Statistik, die sich darauf konzentriert, Daten zu organisieren und zu beschreiben, versucht die Inferenzstatistik, auf der Grundlage von Stichprobenaussagen über eine gesamte Population zu machen.
Konzepte der Inferenzstatistik:
- Parameter und Statistik:
- In der Inferenzstatistik unterscheidet man zwischen Parametern und Statistiken. Ein Parameter ist eine numerische Eigenschaft einer Population (z.B. der Durchschnitt oder die Standardabweichung). Eine Statistik ist eine numerische Eigenschaft einer Stichprobe, die verwendet wird, um auf den unbekannten Parameter der Population zu schließen.
- Hypothese und Hypothesentests:
- Die Inferenzstatistik verwendet Hypothesen, um Aussagen über Populationen zu machen. Ein Hypothesentest beinhaltet die Formulierung einer Nullhypothese und einer Alternativhypothese, Datenanalyse und eine Entscheidung, ob die Nullhypothese abgelehnt wird oder nicht.
- Schätzung und Konfidenzintervalle:
- Schätzungen in der Inferenzstatistik beziehen sich auf Schätzungen von Parametern in der Population basierend auf Stichprobendaten. Konfidenzintervalle geben einen Bereich an, innerhalb dessen der wahre Parameterwert mit einer bestimmten Wahrscheinlichkeit liegt.
- Zentraler Grenzwertsatz:
- Der Zentrale Grenzwertsatz ist ein grundlegendes Konzept in der Inferenzstatistik. Er besagt, dass die Summe oder der Durchschnitt von vielen unabhängigen und identisch verteilten Zufallsvariablen dazu neigt, einer Normalverteilung zu folgen, auch wenn die ursprünglichen Variablen nicht normal verteilt sind. Dies ermöglicht den Einsatz von Normalverteilungseigenschaften bei der Schätzung von Parametern.
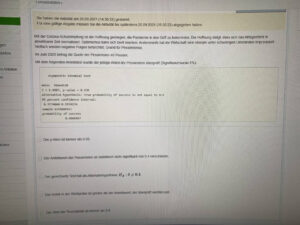
- Signifikanzniveau und p-Werte:
- Das Signifikanzniveau (α) ist der maximale Fehler, den Sie bei der Ablehnung der Nullhypothese akzeptieren würden. Der p-Wert ist die Wahrscheinlichkeit, dass die beobachteten Daten oder etwas Extremeres unter der Annahme wahrer Nullhypothese auftreten. Ein kleiner p-Wert deutet darauf hin, dass die Nullhypothese abgelehnt werden könnte.
- Regression und Korrelation:
- Inferenzstatistik wird in Regressions- und Korrelationsanalysen verwendet, um Beziehungen zwischen Variablen in der Population zu untersuchen.
- Stichprobenverteilungen:
- Die Inferenzstatistik berücksichtigt die Verteilung von Statistiken in wiederholten Stichproben. Dies hilft bei der Beurteilung, wie gut die Schätzung einer Statistik den tatsächlichen Parameter repräsentiert.
Die Inferenzstatistik spielt eine entscheidende Rolle in wissenschaftlichen Untersuchungen, Umfragen, Qualitätssicherung, medizinischen Studien und vielen anderen Bereichen. Sie ermöglicht es, auf der Grundlage von begrenzten Stichproben verlässliche Aussagen über die zugrunde liegende Population zu treffen.
Übungen Inferenzstatistik
- Psychologische Statistik Hypothesenprüfung
- Psychologische Statistik Partialkorrelation Goethe Universität
- Psychologische Statistik Spearman-Rang-Korrelation
Übung Standardisierte Regression
Gegeben: R^2 = 0.87
Zusätzliche Teilaufgaben:
a) Konfidenzintervall für Beta2
b) Wenn rx1x2 = 0.2 ist, wie groß ist dann R^2? R^2 = Beta1^2 + Beta^2 + 2*(Beta1*Beta2*rx1x2)
IU International University of Applied Sciences – Campus Bad Honnef
Skripte Inferenzstatistik
- Skript Inferenzstatistik Universität Osnabrück
- Skript Inferenzstatistik Punkt- und Intervallschätzung Universität Osnabrück
- Skript Inferenzstatistik Hypothesentests Universität Osnabrück
- Skript Inferenzstatistik Power Universität Osnabrück
- Skript Trivariate Lineare Regression
- Skript Mutiple Lineare Regression
- Skript Lineare Regression
Übung p-Werte